来源：中信建投期货微资讯

本报告观点和信息仅供符合证监会适当性管理规定的期货交易者参考。因本平台暂时无法设置访问限制，若您并非符合规定的交易者，为控制交易风险，请勿点击查看或使用本报告任何信息。对由此给您造成的不便表示诚挚歉意，感谢您的理解与配合！

本报告完成时间  | 2023年12月5日

摘 要

随着机器学习和生成式因子挖掘技巧的发展，因子管理和组合成为了研究领域重点专注的方向。本文参考了较新的聚类算法文献综述，从计算机科学的视角整理了实际运用于多个自然科学领域的算法。本文重点关注时序列数据的聚类算法，以及关注多目标下的运用场景。本研究对不同领域的传统和最先进的聚类技术进行了最新的系统和全面的回顾。

由于大多数传统聚类算法仍然依赖于先验提供的聚类数量，因此在聚类方法的选择上，领域专家和实践者都逐渐发生了转变。这些传统的聚类算法不能有效地处理数据对象中聚类数量难以识别的现实数据聚类分析问题。此外，它们不能有效地管理高维数据集的最佳集群数量难以确定的问题。因此，需要改进、灵活和高效的聚类技术。近年来，文献中提出了各种高效的聚类算法，这些算法在实际聚类问题上得到了很好的评价结果。

本文使用了基于分区算法作为method1，在样本外的多套参数中取得了优于等权投票的benchmark的因子合成效果。后续文章我们将进一步探索聚类算法在因子合成中的运用。

风险提示：本报告不构成任何投资建议，期市有风险，入市需谨慎。

一

 背景

随着机器学习和生成式因子挖掘技巧的发展，因子管理和组合成为了研究领域重点专注的方向。本文参考了较新的聚类算法文献综述，从计算机科学的视角整理了实际运用于多个自然科学领域的算法。本文重点关注时序列数据的聚类算法，以及关注多目标下的运用场景。本研究对不同领域的传统和最先进的聚类技术进行了最新的系统和全面的回顾。本文参考了‘A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects’这篇文献综述的分类方法，对于可能运用于因子合成的方法进行了概述。

由于大多数传统聚类算法仍然依赖于先验提供的聚类数量，因此在聚类方法的选择上，领域专家和实践者都逐渐发生了转变。这些传统的聚类算法不能有效地处理数据对象中聚类数量难以识别的现实数据聚类分析问题。此外，它们不能有效地管理高维数据集的最佳集群数量难以确定的问题。因此，需要改进、灵活和高效的聚类技术。近年来，文献中提出了各种高效的聚类算法，这些算法在实际聚类问题上得到了很好的评价结果。

在《CTA 系列六十一：基于相关性的因子合成》中，我们阐述了两种有效的因子合成的尝试。我们基于相关性尝试了两种方案，在原本有效的策略大类下获得了比起等权配置更好的效果。此外，与之前的尝试不同的是，我们使用了日内信号。我们认为，比起固定换仓的日频信号，对于日内策略进行统计学上的处理效果应该更为有效。我们选取了持仓频率高低不一的日内策略组合6个进行实践。

在《CTA 系列六十五：基于相关性的因子合成（二）运用篇》中，我们按第一期因子合成方法所述，因子合成往往有两个运用场景，第一个场景是对于某一类利用类似逻辑的因子组（或者可能仅仅是为了追求参数稳定性而生成的多套参数因子组）进行组合；第二个场景是对于一些具有不同逻辑的因子组进行合成。基于我们做的很多前期尝试，我们发现等权合成往往是性价比最高的合成方式，超过了一些基于复杂机器学习的因子合成方式，也超过了基于因子绩效和回撤来做择时的传统方式。我们一直在寻找逻辑简单可行而且超出等权合成的方式。在之前的报告中，我们的重点在于第二个场景，对于大类策略进行合成；这次我们的重点在于第一个场景。我们希望观察对于原本有一定预测能力的因子群，是否能够击败等权配置。

本文是因子合成的第三篇，重点在于实践。我们使用了自设的自下而上的因子组合方法，将给定的170个因子进行合成，总共得到65个类别，在样本外取得了超越benchmark的效果。

二

 实战案例

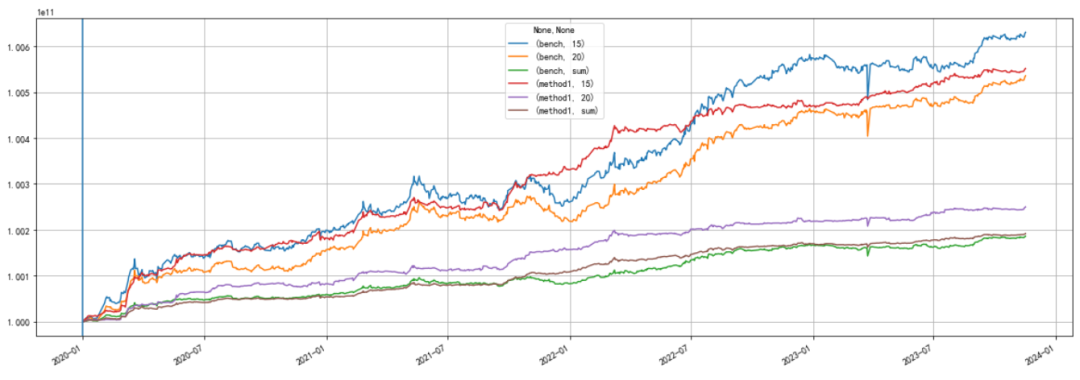
表中bench指未使用任何合成方法，而是使用投票方式决定最终信号，15指超出15%的投票偏向一侧时则给出对应信号。Sum指不使用投票，而是直接使用信号均值作为最终信号。Method1是我们使用的合成方法，具体内容将在后续文章中揭晓。

三

 层次和分区的聚类算法介绍

3.1. 层次聚类 hierarchical

层次聚类算法是一种基于距离的聚类方法，它允许我们根据数据对象之间的相似性将它们划分为不同的级别。这种算法通过迭代地形成集群，从而生成一个描述聚类层次结构的树状图。在层次聚类中，我们可以通过将单个点之间的距离泛化为点的子集之间的距离来完成点的合并或分割。这是通过使用称为联系度量的接近度量来确定的。

层次聚类中使用了三种基本的链接度量：单个链接、平均连接和完整链接。这些链接度量用于构建用于聚类的二进制或二进制连接矩阵。相似矩阵的构造是通过寻找每对数据点之间的相似度来实现的。然后，通过查找聚类之间的成对距离来计算连锁准则。相似性度量用于确定聚类集之间的距离，也用于确定cluster的形状。

层次聚类算法具有处理任何相似度量和灵活的粒度级别的能力，因此适用于任何属性类型。然而，这种方法也存在一些缺点。首先，由于其计算复杂度较高（至少为 O(N^2)），它在大规模数据集中的应用受到限制。其次，层次聚类方法可能受到不可逆的分裂或合并过程的影响，这使得无法重新访问已经制定的聚类来重新分配错误分配的对象。此外，层次聚类方法还存在终止标准的模糊性和对噪声和异常值的敏感性问题。

3.2. 分区聚类 partitional

分区聚类算法从初始数据集分区开始，迭代地将数据点或模式分配到聚类中，以减少平方误差。可以从模式矩阵中随机选取K个彼此分离良好的种子点作为初始分区。Nagpal(2013)指出，如果选择的初始点来自现有数据对象，并且彼此之间距离足够远，则可以确定好的随机种子点。随着集群数量的增加，平方误差趋于减少，并且这种最小化只能在固定数量的集群中实现。在一些算法中，分割聚类中的平方误差准则函数使生成的K个编号的聚类尽可能紧凑和分离。与其他准则函数相比，它的计算需求更少(Jain and Dubes，1988)。因为基于平方误差的算法可以收敛到局部最小值，不同的初始分区可以产生不同的集群作为输出，特别是如果初始点没有很好地分离(Nagpal，2013)。根据(Jain 和Dubes，1988)，分区技术经常用于工程应用程序中，其中单个分区最重要，并且适合于有效地表示和压缩大型数据库。还观察到，由于可用数据的性质，分区算法在模式识别中更受青睐(Jain，2010)。分割聚类方法是一种局部搜索技术(Khaled et al.，1995)和局部收敛技术。因此，不能保证全局最优解(Sanse和Sharma，2015)。

分区的聚类是一个NP-hard优化问题，其标准方法是找到近似解(Harshada et al.，2015)。Jain 等人(1999)指出，“对一组可能的标签进行组合搜索，以获得标准函数的最优值，这在计算上是令人望而却步的”。因此，典型的分区聚类算法以不同的起始分区运行多次，从而选择所有运行中给出最佳聚类输出的一个作为最优解 Jain et al.(1999)。分区聚类算法的一个主要缺点是需要为参数