摘 要
本文探讨了经典互换定价方法在人民币利率互换市场的适用性。研究认为,人民币利率互换定价应该用无风险利率贴现,此时经典定价方法中“参考利率和贴现率为同一无风险利率”的假设未必成立,不能简单套用经典方法对参考利率与无风险贴现率不一致情况下的互换进行定价。对此,本文提出了相对精确的互换定价模型,并对误用经典定价方法产生的误差展开实证分析。
关键词
利率互换 贴现率 等价鞅方法 动态利率期限结构模型
众所周知,金融资产的价值等于未来现金流期望值的合理贴现。在人民币利率互换市场上,FR007利率互换和Shibor3M利率互换通常采用远期利率计算未来现金流的期望值,并用各自的参考利率作为贴现率。这一做法是否合理?如果不合理,应该如何定价?如果采用这一不合理做法,会产生多大的定价误差?本文试图就这些问题展开讨论。
经典定价方法:基于定价原理的探析
常见的利率互换是合约双方约定在未来的一定期限内,根据约定数量的名义本金彼此交换基于给定参考利率计算的浮动利息和固定利息的金融合约。实际上,利率互换既可以视为一个浮息债和固息债的组合,也可以视为一系列远期利率协议(FRA)的组合,相应地,互换定价问题可以转化为债券定价或FRA定价问题(陈蓉和郑振龙,2021)。
以FRA定价法为例,其假设互换合约中的参考利率与其合理贴现率不仅要一致,且均须为无风险利率。因为互换合约中拆分出来的单个FRA定价看似简单,其实质却是在一个特定的远期测度下定价。以t 时刻名义本金为N、协议利率为K、远期期限为Ti-Ti-1 的FRA 合约为例,其合约价值为
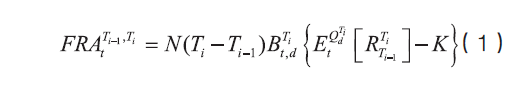
其中,
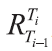
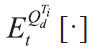
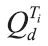
Ti远期测度
Ti-1到Ti时刻的即期利率,
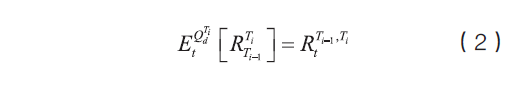
相应地,FRA价值才可以表示为
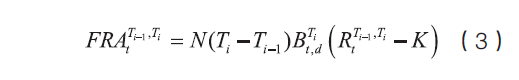
如果参考利率不是无风险利率,则(1)~(3)式不再成立,
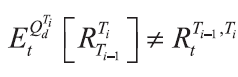
经典定价方法不再适用。
在2007年美国次贷危机发生前,国际市场上利率互换合约的主流参考利率和贴现率都为LIBOR,并且市场默认LIBOR为无风险利率。然而,次贷危机爆发后,LIBOR不再能反映真实的市场无风险借贷利率,经典定价方法不再成立。那么经典定价方法在我国市场上是否适用?为了回答这一问题,需要考虑互换合约中的参考利率与其合理贴现率是否都为无风险利率。
(一)合理贴现率
由于我国于2009年正式推出NAFMII主协议,引入了诸如单一协议、终止净额、履约保障等重要机制和概念,有效降低了交易双方的信用风险。参与国内银行间互换交易的双方均应签署上述文件,故可以认为人民币利率互换的贴现率中不需要包含对手违约风险溢价。
此外,参考利率的信用风险和流动性风险是由生成参考利率的银行间市场信用和流动性决定的。而利率互换交易者并不与生成参考利率报价的银行间市场成员直接交易,因此参考利率的市场风险不会改变利率互换交易双方本身的信用风险,不应该反映在贴现率上。
基于上述两点考虑,在人民币利率互换市场上,合理的贴现率应为无风险利率。
(二)参考利率
由于我国利率互换市场上存在多种参考利率,如果其中之一被认为是无风险利率,则其他利率就不可能是无风险利率。以我国市场主流的FR007利率互换和Shibor3M利率互换为例,如果假设FR007更接近无风险利率,那么FR007利率互换采用经典定价方法就没有问题,但是Shibor3M利率互换采用经典定价方法则会产生误差,因为此时不能继续用Shibor远期利率代替无风险Ti远期测度下未来Shibor即期利率
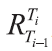
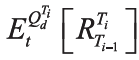
相对精确的互换定价模型:测度转换方法
如果参考利率不是无风险利率,此时只能回到定价式(1)对互换定价:
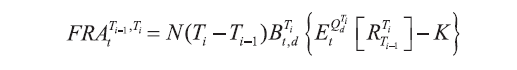
其关键在于估计
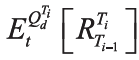
首先,假设
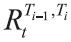
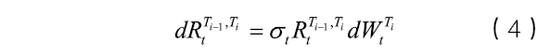
其中,σt表示
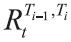
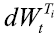

其次,参考Bianchetti(2010),无风险贴现因子
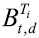
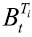
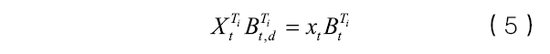
易知
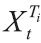
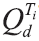
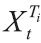
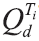
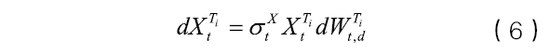
其中,
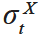
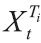
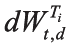
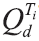
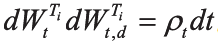
最后以
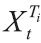
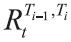
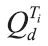
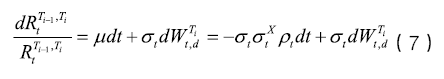
即可求得
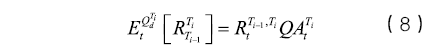
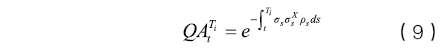
从而得到FRA相对精确的定价公式为
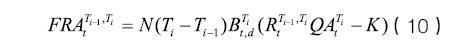
相对精确的互换利率表达式则为
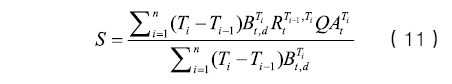
误用经典定价方法:误差有多大?
本节以Shibor3M利率互换为例,探索误用经典定价方法可能造成多大的误差。
(一)误用经典定价方法
经典互换定价方法下Shibor3M互换利率为
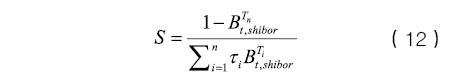
其中n为到期前付息次数(季度付息),τi代表每一付息期之间的时间间隔。根据贴现因子和远期利率的关系,就可以得到互换隐含远期利率
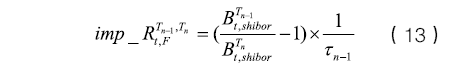
(二)相对精确的方法
对式(12)略微变形可得到相对精确的互换隐含远期利率公式应为
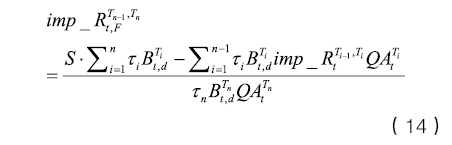
显然,
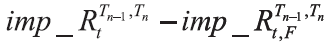
(三)实证结果
1.实证数据
本文基于2012年5月21日至2022年11月18日的Shibor3M利率互换曲线展开实证分析。本节采用国开债即期利率作为无风险利率的代表。在构建Shibor曲线时,对于1年期以下的部分使用市场现有的Shibor报价来度量;对于1年期及以上的部分使用AAA级商业银行普通债即期利率来近似度量1。
2.计算定价误差
(1)错误的互换隐含远期曲线
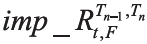
将Shibor3M利率互换曲线数据代入公式(12)~(13)中,就可以得到不同期限的互换隐含远期利率
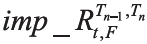
(2)相对精确的互换隐含远期曲线
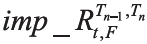
首先从国开债即期利率曲线中计算出无风险贴现因子
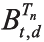
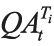
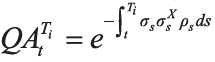
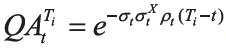
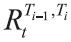
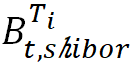
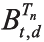
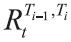
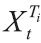
ρt通过Shibor远期利率
σtX通过Shibor贴现因子
σt、σtX、ρt在任意时刻都具有水平的期限结构,从而将等式化简为
算出
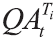
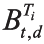
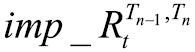
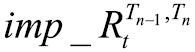
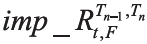
3.分析结果
根据上述过程计算出误用经典方法造成的误差如表2所示。
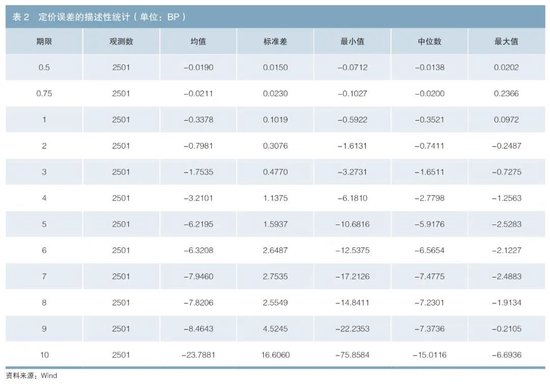
由表2可知,定价误差整体为负值,这表明误用经典方法总体会高估远期利率,并且误差随期限的增大而增大,当期限为10年时,误用经典方法带来的最大误差可以达到近76BP。
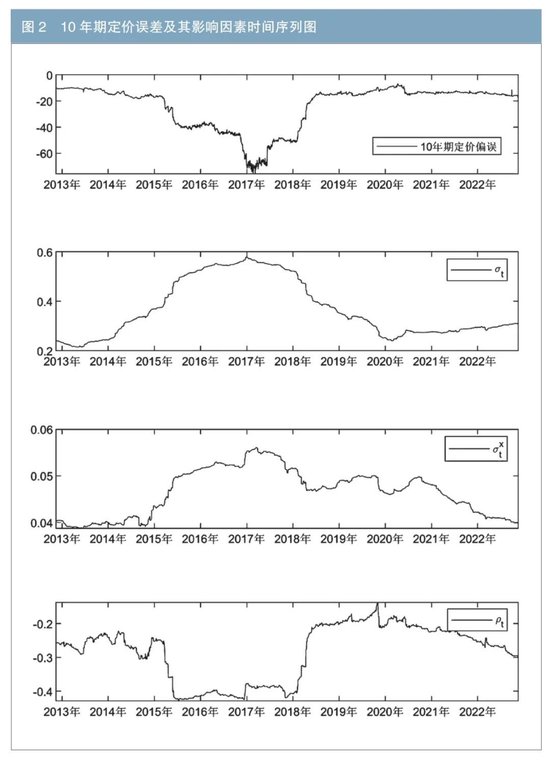
笔者进一步以10年期定价误差时间序列为例,结合σt、σtX、ρt的走势分析定价误差变化的原因(见图2)。可以看出,当远期参考利率波动率σt较大时,转换因子的波动率σtX通常也处于较高水平,一旦远期参考利率和转换因子的相关系数ρt发生突变,使用经典方法可能会造成较大的定价误差。
总结
文章提出了参考利率和无风险贴现率不一致情况下相对精确的互换定价模型。基于Shibor3M利率互换数据的实证研究表明,误用经典定价模型会产生较大的误差。这种误差与参考利率曲线和无风险利率曲线的波动性以及二者的联动性正相关,并且随互换期限的增长而迅速扩大。该发现能对实践中合理估计互换价值提供有效参考。
注:
1.经测算Shibor与同期限AAA级商业银行普通债即期利率具有非常相近的时间序列走势,因此不会对后续实证结果造成太大误差。
参考文献
[1]陈蓉,郑振龙. 固定收益证券[M].北京:高等教育出版社,2021.
[2]Bianchetti M. Two curves, one price: pricing & hedging interest rate derivatives decoupling forwarding and discounting yield curves[J]. Risk, 2010, 23(8): 66—72.
◇本文原载《债券》2023年6月刊
◇作者:厦门大学管理学院财务系 金婕雯 陈蓉 竺添晟
◇ 编辑:赵丽 张轶龙 印颖